이번 EMNLP 2019에서 Graph Neural Network(GNN) 튜토리얼 세션이 진행되었습니다. 그 중 가장 처음으로 소개되었던 Semi-Supervised Classification with Graph Convolutional Network(ICLR 2017)을 살펴보고자 합니다. 본 논문에서는 아래 그림과 같이 그래프와 그래프의 몇몇 노드들에 주어진 레이블을 이용하여 나머지 노드들의 레이블을 예측하는 그래프 노드의 semi-supervised classification 문제를 풀고자 합니다.
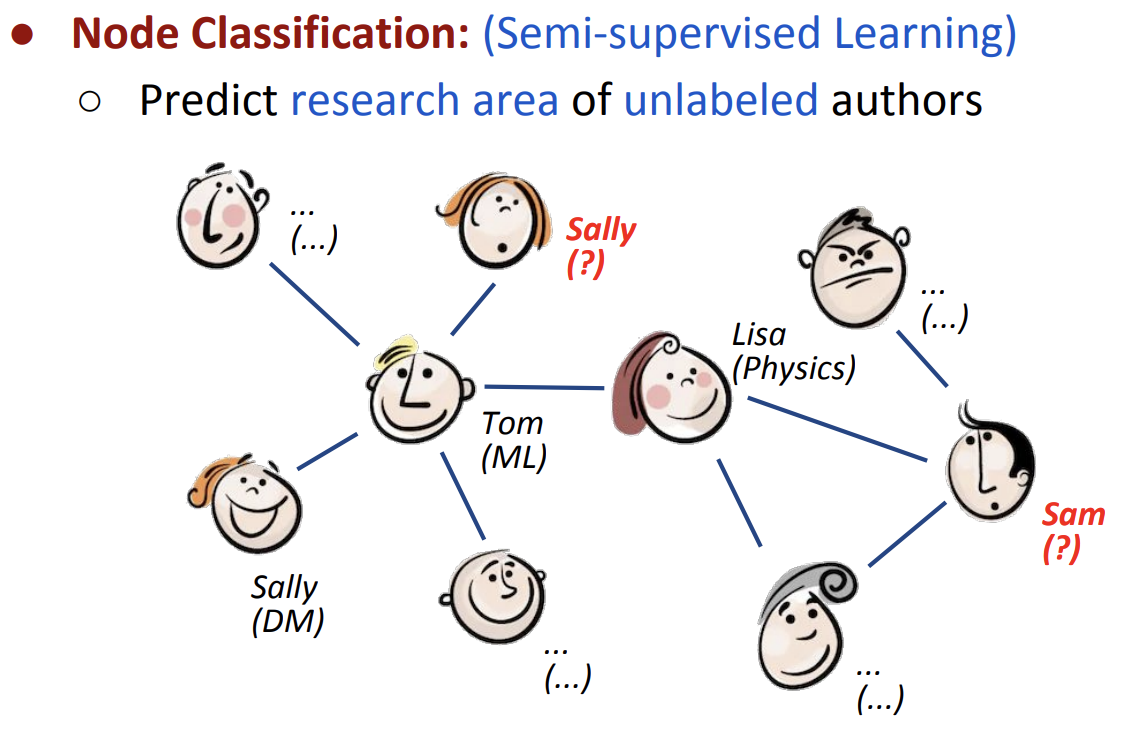
Main Idea
-
그래프 각 노드의 Feature \(X\)와 인접 행렬 \(A\)가 주어졌을 때, 이를 이용하여 분류 문재를 푸는 Multi-layer Graph Convolutional Network(GCN), \(f(X, A)\)을 제시합니다. 또한 이 방법이 spectral graph convolution의 빠르고 효율적인 1차 근사임을 증명합니다.
-
이전의 semi-supervised 조건의 연구들에서는 \(L = L_0 + \lambda L_{reg}\) 와 같은 loss의 형태로 학습을 진행했습니다. 여기서 \(L_0\)는 label이 있는 노드에 대한 classification loss이고, \(L_{reg}\)는 Graph Laplacian regularization term으로, 연결된 노드가 비슷한 representation을 갖도록 하는 loss입니다. 하지만 이는 연결된 노드는 유사하다는 가정(동일한 label을 가질 확률이 높음)을 갖고 있기 때문에, 유사도 이외의 추가적인 정보를 담지 못하게 되어 모델의 능력을 제한합니다. GCN에서는 인접행렬을 입력으로 이용하여 어떤 노드들이 연결되어 있는지에 대한 정보를 직접적으로 이용함으로써, 이 제한을 해결하고자 합니다.
Graph Convolutional Networks(GCN)
본 논문에서는 그래프와 인접행렬을 모델의 입력으로 이용하는 GCN, \(f(X,A)\)를 제시합니다. 이 모델은 다음과 같은 Graph Convolution 연산을 여러 번(Multi-layer) 진행합니다.
\[H^{(l+1)} = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})\]- \(H^{(l)}\): \(l\)번째 layer의 Hidden state이며, \(H^0 = X\)(그래프 노드의 초기 feature) 입니다.
- \(\tilde{A}\): \(A + I_N\) 으로, 인접행렬(\(A\))에 자기 자신으로의 연결(\(I_N\))을 추가한 것입니다.
- \(\tilde{D}\): \(\tilde{D}_{ii} = \sum_{j} \tilde{A}_{ij}\) 로, 각 노드의 degree를 나타내는 대각 행렬입니다.
- \(W^{(l)}\): \(l\)번째 layer의 학습가능한 parameter입니다.
- \(\sigma\): 비선형 함수로 \(ReLU(\cdot)\)를 이용했습니다.
예시를 통해 위 수식의 의미를 따라가보면 다음과 같습니다.
-
노드 4개로 구성된 (undirected, unweighted)그래프에서 인접행렬(\(A\) 및 \(\tilde{A}\))과 degree 행렬(\(D\) 및 \(\tilde{D}\))을 얻을 수 있습니다.
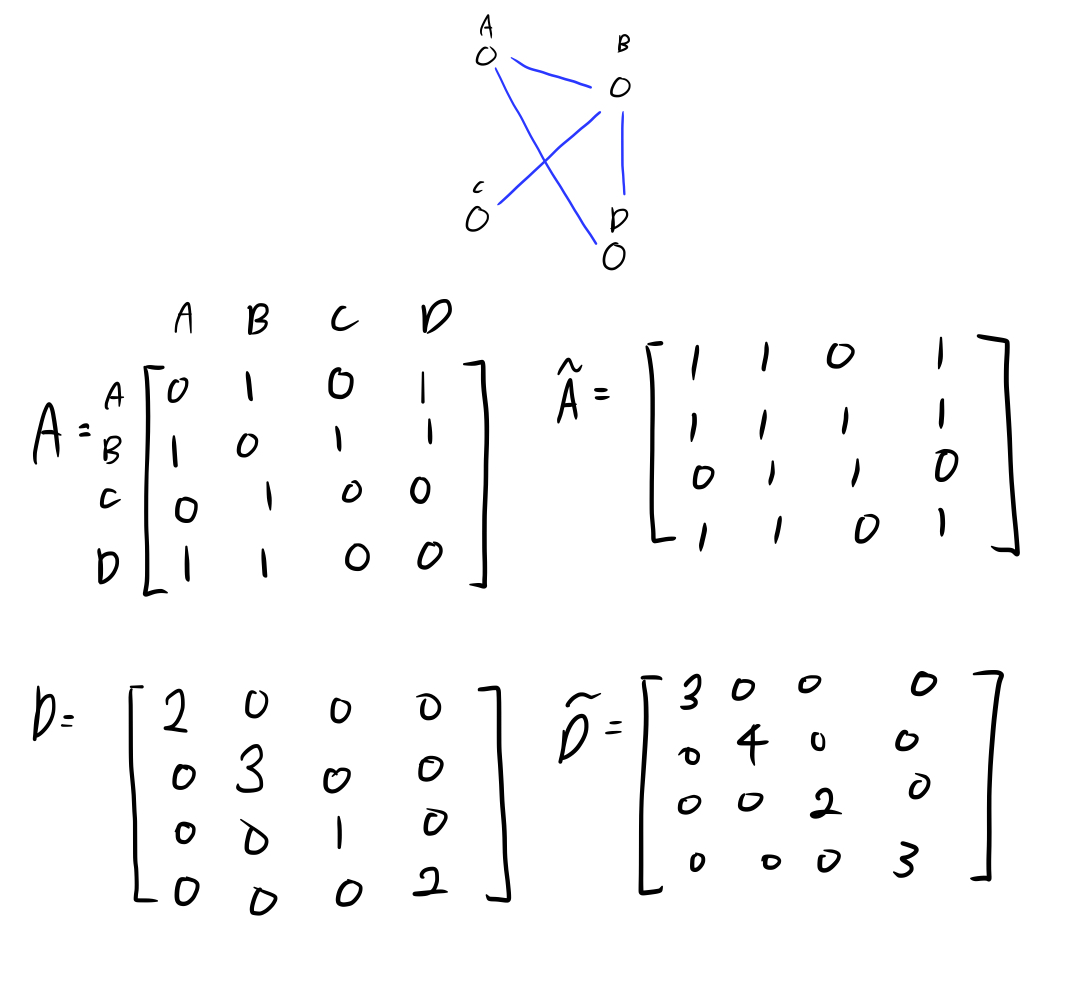
-
\(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}\)를 계산하면 아래와 같은데, 각 노드에 연결된 edge의 갯수에 따라 인접행렬(\(A\))을 정규화(normalization)합니다. 이는 학습을 진행할 때, 각 노드별 edge의 갯수에 관계없이 모든 노드들을 잘 학습하기 위한 과정으로 볼 수 있습니다.
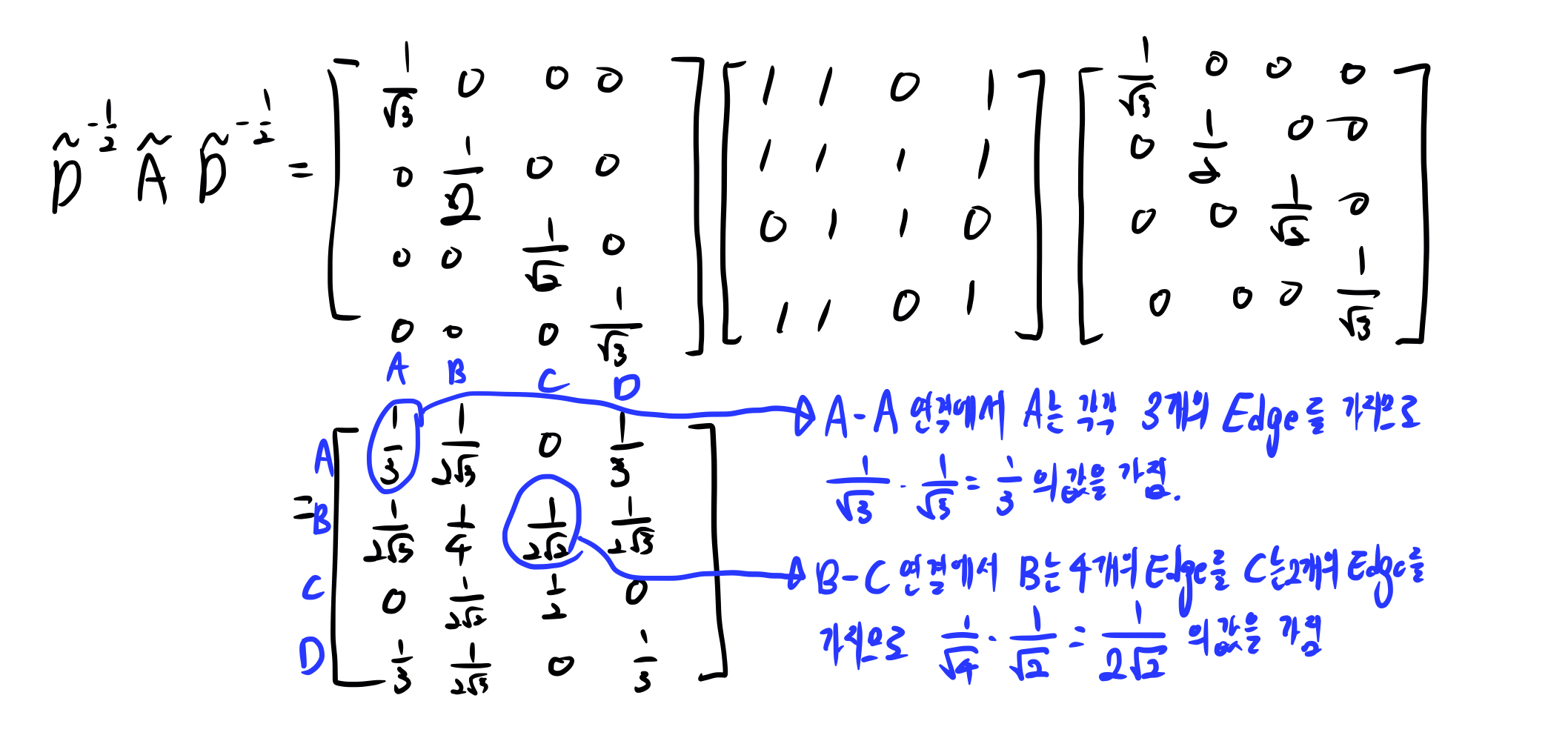
-
2번 과정에서 계산한 \(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}\)를 이용하여 \(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}, l=0\)를 계산하면 아래 그림과 같습니다. 여기서 \(H^{l}\)은 \(l\)번째(이전 레이어의) hidden state이고, \(l=0\)인 경우 초기 값은 각 노드의 초기 feature vector가 됩니다. 예시로 각 노드가 특정 단어인 경우 word embedding vector를, 각 노드가 문서인 경우 bag-of-word vector를, 가장 간단하게는 전체 노드 개수의 길이를 갖는 one-hot vector를 이용할 수도 있습니다. 이 식을 계산하면, 각 행은 각 노드에 연결된 노드들(자기자신을 포함한)의 초기 feature 값들(or 이전 hidden state)들의 가중 합이 됩니다. (가중치는 2번과정에서 계산한 각 노드별 edge개수에 따라 normalize된 값입니다.)

-
3번과정의 결과물과 학습가능한 parameter \(W^{(l)}\)을 곱합니다. 이를 통해 아래 그림과 같이 각 노드별로 인접 노드들의 가중치 * 초기 feature vector * W의 합을 갖게 됩니다. 결과적으로 GCN은 특정 노드의 representation으로 해당 노드에 연결되어 있는 노드들을 가중합하는 방법입니다.
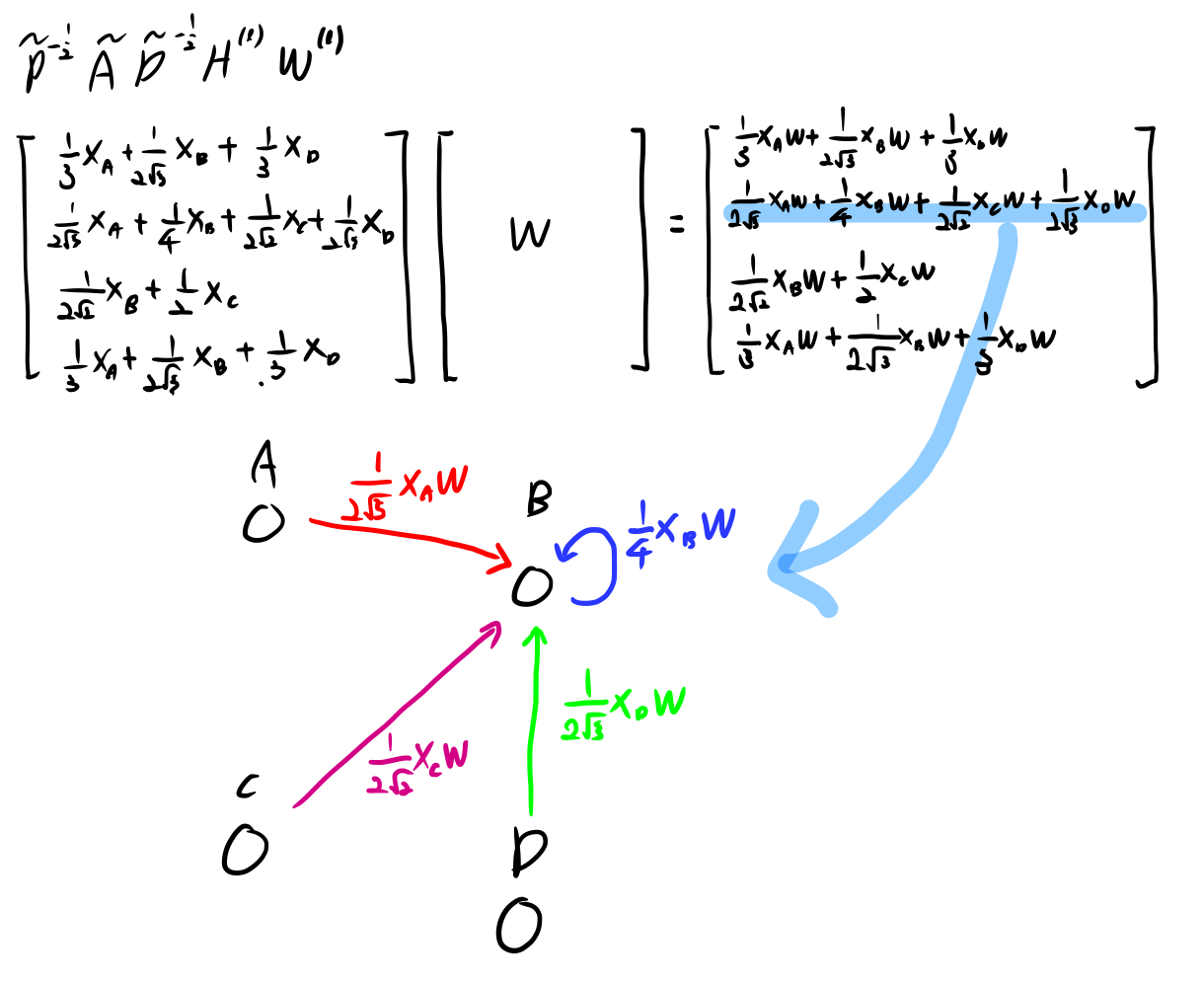
-
마지막으로 4번 결과물을 비선형함수(\(\sigma\))를 통해 비선형성을 학습할 수 있도록 했습니다.
이 layer가 하나일 때는 각 노드들의 인접한 노드들만 이용하여 hidden state를 계산합니다. 하지만 이 layer를 K 개 쌓으면, 해당 노드에서 K개 떨어져 있는(K개의 edge를 갖는) 노드 까지 이용한 hidden state를 계산할 수 있습니다. 이를 통해, label이 있는 노드가 적더라도, 해당 노드에서 K개 떨어져있는 노드까지 고려하여 학습을 진행할 수 있습니다.
Experiments
1. Model
\[Z = f(X,A) = softmax(\tilde{A} ReLU(\tilde{A}XW^{(0)})W^{(1)})\]본 논문에서는 위 식과 같이 2-layer GCN으로 진행되었습니다. \(A \in \mathbb{R}^{N \times N}\), \(X \in \mathbb{R}^{N \times D_0}\), \(W^{(0)} \in \mathbb{R}^{D_0 \times D_1}\), \(W^{(1)} \in \mathbb{R}^{D_1 \times D_2}\), Classification 문제를 풀기 위해 \(D_2\)은 Class의 갯수가 됩니다. 비선형 함수로 첫 번째 layer에서는 ReLU, 두 번째 layer에서는 classification을 위해 Softmax를 이용했습니다.
그리고 label이 있는 학습 데이터(\(Y_L\))에 대해 다음과 같이 loss를 계산했습니다.
\[L = - \sum\limits_{l \in Y_L}\sum\limits^F_{f=1}Y_{lf}lnZ_{lf}\]2. Dataset
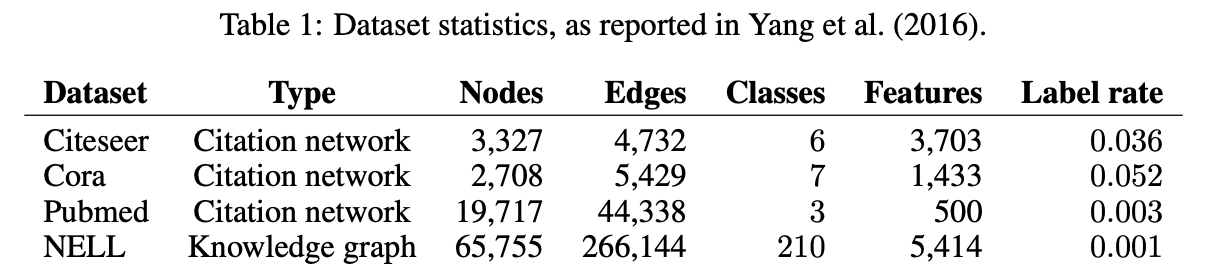
실험을 위해 위의 그림과 같이 두 가지 종류(Citation network, Knowledge graph)의 Graph dataset을 이용했습니다.
- Citation network: 각 노드는 문서이고 edge는 citation link입니다. labeled node는 총 노드 중 학습 셋에서 label이 있는 노드의 비율입니다. 각 노드의 초기 feature로는 각 문서의 bag-of-words vector를 이용했습니다. 학습 시 각 class에 대해 20개의 label data를 이용하여 학습을 진행했습니다.
- NELL: NELL은 Knowledge graph로 부터 추출된 biparitite graph(이분 그래프)입니다. 이 데이터는 (\(e_1, r, e_2\)) 와 같이 특정 entity들과 그 사이의 관계(relation)를 갖고 있습니다. 저자들은 이를 표현하기 위해 relation 노드를 만들어 (\(e_1, r, e_2\))를 (\(e_1, r_1\)), (\(e_2, r_2\))와 같이 나타냈습니다. 따라서 노드는 entity와 relation 노드로 구성되며, 각 노드의 초기 feature로 enitiy 노드의 경우 sparse feature vector, relation 노드의 경우 relation에 대핸 one-hot vector를 이용했습니다.
3. Setup
- 1000개의 labeled 데이터에 대해 test accuracy를 측정했습니다.
- hyper parameter 선택을 위해, 500개의 labeled 데이터를 validation set으로 이용했습니다.
- 200epoch까지 학습했고 window size 10, validataion loss로 early stopping 했습니다.
- Adam optimizer(lr=0.01)를 이용했고, Full-batch optimization으로 전체 데이터 셋에 대해 한번의 backward optimize를 진행했습니다.
- hidden size(\(D_1\))는 Citation dataset에서는 16, NELL에서는 64를 이용했습니다.
4. Results
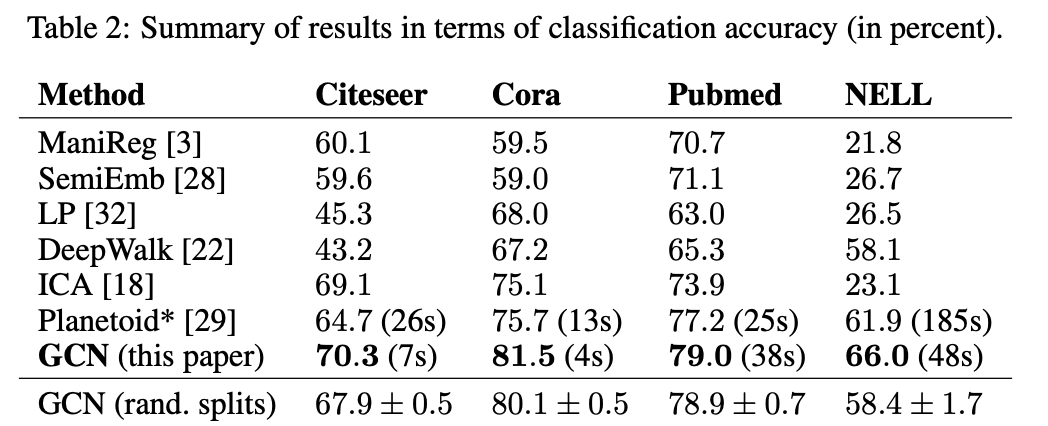
저자들은 동등한 비교를 위해 이전 SOTA 모델(Yang et al., 2016)과 동일한 데이터 split을 이용했고, initialize를 다르게 한 100개의 모델 결과를 평균하였습니다. 그리고 이전 모델들에 비해 우수한 결과를 얻을 수 있었습니다. GCN(rand. splits)는 10개의 랜덤으로 뽑힌 같은 크기의 학습 데이터셋으로 학습했을 때, 평균과 표준편차를 나타냅니다.
본 리뷰에서는 작성하지 않았지만, ICLR paper답게 본 논문에서 제시한 GCN이 spectral graph convolution의 빠르고 효율적인 1차 근사임을 수식으로 증명하는 과정이 등장합니다. 또한 각 중간 과정의 수식으로 학습을 진행했을 때의 결과또한 제시되어 있고, 최종적으로 GCN에서 사용한 방법이 가장 좋은 성능을 보였습니다.
Limitation and Future Work
-
Memory requirement: Full-batch gradient descent 방식을 이용했기 때문에, dataset의 크기에 따라 memory 요구량이 늘어납니다. 따라서 mini-batch gradient descent 방법을 이용해야 하는데, K 개의 layer가 있는 경우 mini-batch 에 포함된 노드들의 K 번째 이웃 노드들 또한 메모리에 가지고 있어야 하는 점을 고려해야 합니다.
-
Directed edges and edge features: 본 논문의 방식은 edge features(relation 등)을 고려하고 있지 않고, undirected graph에만 적용가능합니다. 하지만 NELL의 결과에서 보였듯이, directed edge와 edge feature는 (relation node와 같은) 추가적인 노드들을 이용하여 undirected bipartite graph 형태로 나타낼 수 있었습니다.
appendix
appendix 중 layer의 깊이에 따른 실험이 흥미로운 결과를 보였습니다. GCN layer의 갯수를 1부터 10개까지 늘려가며 실험을 진행했는데, 추가적으로 다음과 같이 Residual connetction을 추가한 모델도 함께 이용했습니다.
\[H^{(l+1)} = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) + H^{(l)}\]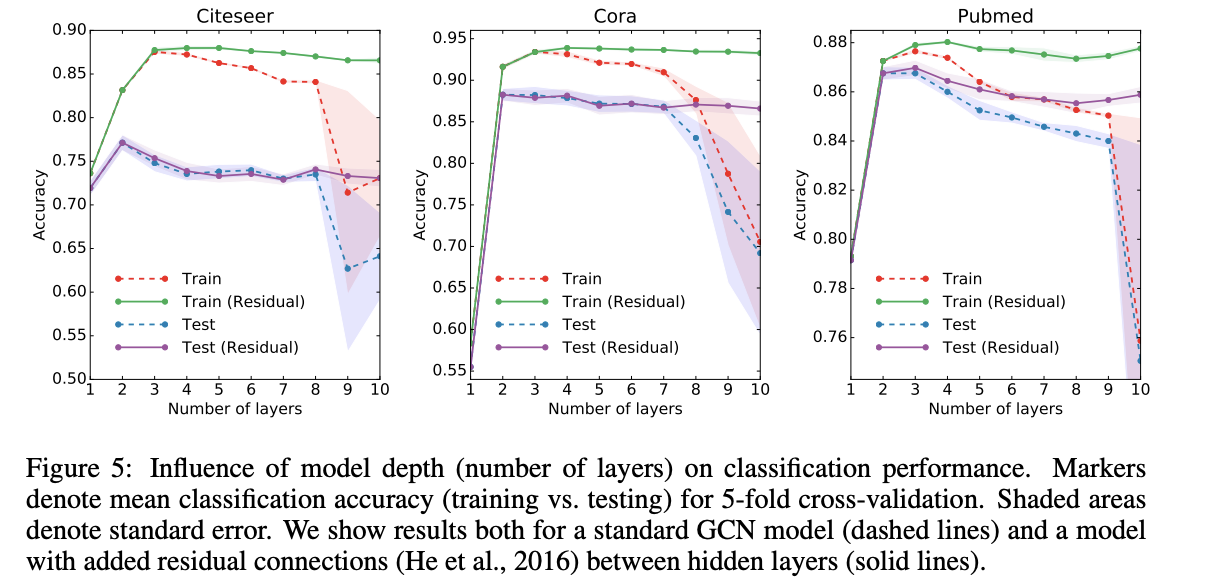
위 그림의 결과를 보았을때, 가장 좋은 결과는 2~3개의 layer를 이용한 경우입니다. 또한 7개 이상의 layer를 쌓은 경우, residual connection 없이 학습을 진행하면, 학습이 어려워 지는 것(optimize가 힘들어 지는 것)을 볼 수 있습니다. 또한 layer수가 많아 지면, parameter가 많아지고 overfitting 문제가 발생할 수도 있습니다.
Reference
-
Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. International Conference on Learning Representations (ICLR), 2017
