BERT기반의 모델들(XLNet, ALBERT 등)은 여러 NLP 테스크에서 좋은 성능을 보여주고 있지만, 이들 각각은 거대한 파라메터들로 구성되어 있습니다. 그래서 리더보드에 등록되어있는 크기의 모델들(일반적으로 Base/Large 모델들)은 서비스에 바로 적용하기에 무리가 있습니다. (BERT의 경우 이를 위해 더 작은 크기의 모델을 공개했습니다.) 최근에는 이를 해결하기위해 다양한 경량화 방법들이 연구되어지고 있는데요, 크게 Knowledge Distillation, Pruning, Quantization 3가지 종류의 방법으로 나눌 수 있습니다. 이번 포스트에서는 새로운 Pruning 방법을 이용하여 BERT 경량화를 진행한 “schuBERT: Optimizing Elements of BERT(ACL 2020)”를 리뷰하겠습니다.
1. Main Idea
BERT기반의 모델들은 트랜스포머 인코더를 이용합니다. 트랜스포머 인코더는 레이어 수나 각 레이어의 크기 등 몇몇 하이퍼파라메터를 통해 구성되는데요, 일반적으로 모델의 크기를 줄이기 위해서는 이 하이퍼 파라메터를 임의로 줄여서 학습된 모델을 이용합니다. 본 논문에서는 이렇게 구성된 하이퍼파라메터들이 충분히 최적화되지 않았다고 제안합니다. 이를 해결하기 위해 1) 하이퍼 파라메터를 더 세분화하여 가능한 모델 구조 수를 늘리고 2) 프루닝기반의 기법으로 제한된 파라메터 크기 내에서 구조 자체를 최적화합니다. 결과적으로 BERT-base를 제안한 방법으로 프루닝 했을 때, 동일한 파라메터 크기를 갖는 모델들 보다 우수한 성능을 보였습니다.
2. Hyperparameters of BERT
BERT는 양방향 트랜스포머 인코더 구조를 갖고 있습니다. 트랜스포머 인코더는 다음과 같은 하이퍼파라메터로 구성됩니다. 본 논문에서는 이를 레이어를 디자인하는 차원으로 언급합니다.(따라서 기존 BERT는 3차원의 디자인 차원으로 구성되어 있습니다.)
- \(l\): 인코더 레이어의 수(트랜스포머 블록의 수)
- \(h\): 트랜스포머 블록의 히든 사이즈
- \(a\): 트랜스포머 블록의 Multihead Attention에서 head의 수
이에 따라 다양한 크기의 트랜스포머 인코더를 만들 수 있고, 일반적으로 Base(\(l=12\), \(h=768\), \(a=12\), 108M)와 Large(\(l=24\), \(h=1024\), \(a=16\), 340M) 크기의 BERT가 많이 이용됩니다. Large 크기의 모델은 Base에 비해 더 높은 성능을 보이지만 비교도 안될정도로 많은 파라메터 수로 인해 실제로 사용하기에 무리가 있습니다. 그리고 Base 크기의 BERT는 동일한 파라메터를 갖는 설정에서 GPT, ELMo 에 비해 좋은 성능을 갖기 때문에 널리 이용되고 있습니다.
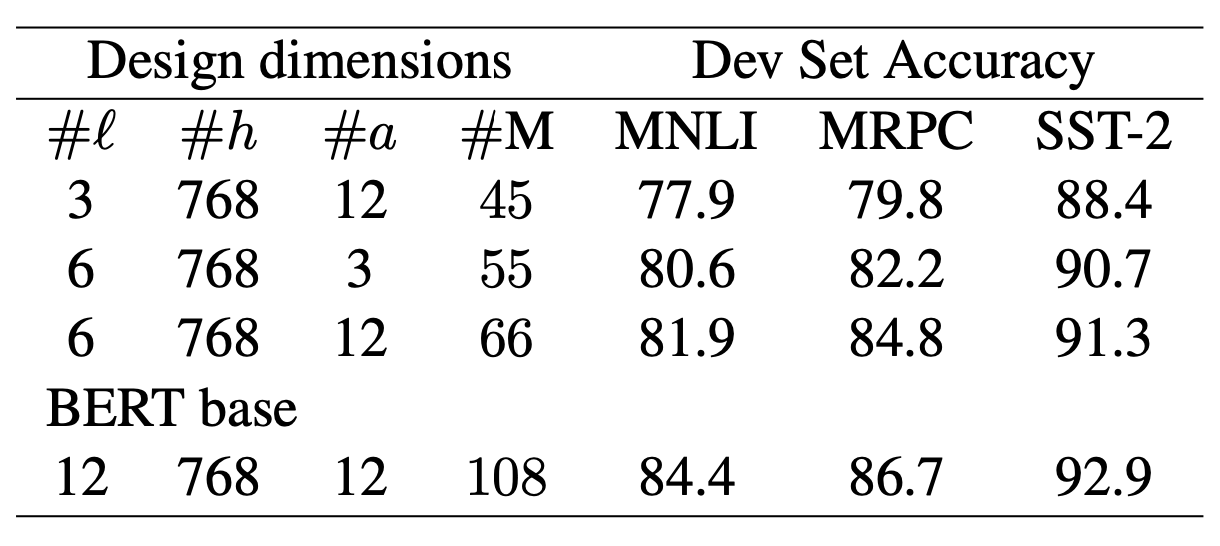
BERT의 논문의 실험 결과(위 표)에서 보여지듯이, 위의 하이퍼파라메터들-레이어 수(\(l\))와 Attention head의 수(\(a\))는 감소할수록 모델의 성능도 급격하게 하락합니다. 본 논문에서는 위에서 제시한 하이퍼파라메터 외에 성능의 큰 하락 없이 모델의 크기를 줄여줄 수 있는 새로운 변수를 찾고자 했습니다.
3. The Elements of BERT
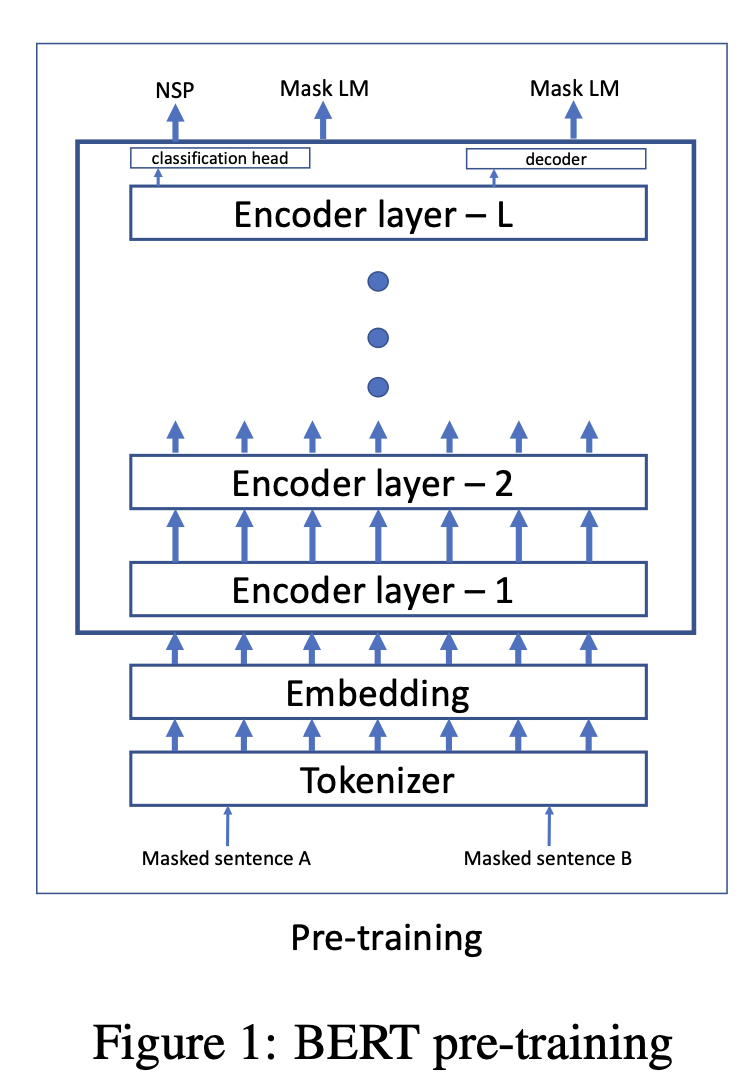
BERT는 위 그림과 같이 입력 토큰들의 임베딩 백터(\(h\) 차원)가 인코더 레이어(\(1~l\))를 순차적으로 통과하여 contextualized representation을 얻습니다. pre-training 단계에서는 [CLS] 토큰의 출력값을 이용하여 NSP문제를, 각 토큰의 출력값을 이용해 MLM문제를 풉니다.
BERT의 구성요소는 사전에 제시한 하이퍼 파라메터(\(l, h, a\))와 다음과 같은 규칙들을 따라 구성됩니다.
- 트랜스포머는 Multi-head Attention에서 고정된 크기(\(h/a\))의 Key, Query, Value를 이용하여 연산을 진행합니다.
- 각 Head의 Attention을 진행하기 전에 통과되는 FeedForward의 경우, \(hidden \space size \times attention \space head\) 차원으로 계산됩니다.
- 모든 레이어는 동일한 크기(하이퍼 파라메터)의 트랜스포머 블록입니다.
- intermediate(attention 연산 이후의 FeedForward)의 차원은 \(4 \times hidden \space size\)로 계산됩니다.

Bert-base기준 위 표와 같이 \(l=12, h=768, a=12\)를 갖고, \(f, k, v\)의 경우 \(h,a\)의 함수로 구성됩니다. 인코더의 각 레이어(트랜스포머 블록)는 동일한 \(a, f, k, v\)로 구성되어 크기가 같습니다.
본 논문에서는 이러한 BERT의 구성요소(디자인 차원)를 다음과 같이 세분화(일반화)합니다.
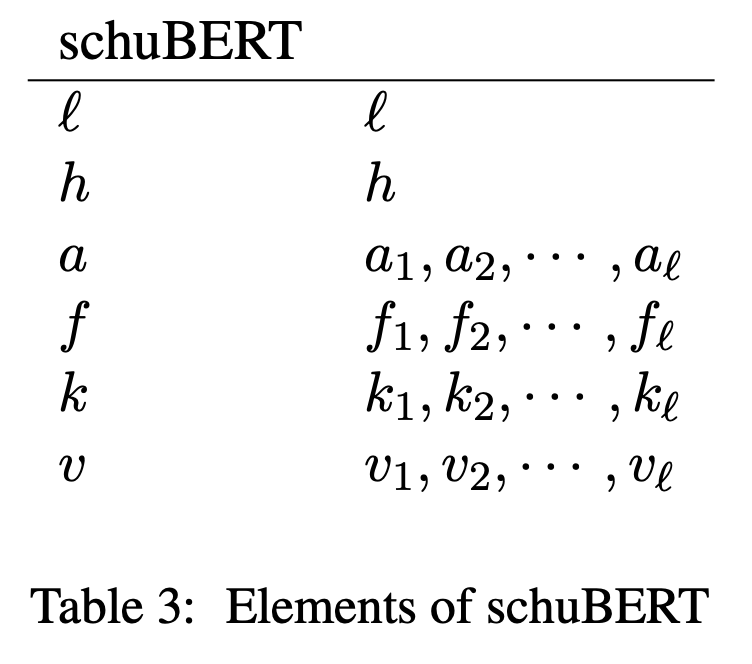
- \(k, v\) 는 항상 \(h/a\)로 같았지만 실제로 Attention연산에서는 두 차원이 달라도 되므로 이를 분리합니다.
- \(f, k, v\)를 \(l, h, a\)에 의존하는 것(원래의 BERT)이 아닌 독립적인 구성요소로 다룹니다.
- 각 레이어 별로 동일한 \(a, f, k, v\)를 갖는 것(원래의 BERT)이 아니라 \(a = a_1,a_2,...a_l\) 와 같이 레이어 마다 다른 값을 갖습니다.
즉 원래 BERT 디자인의 차원을 3차원(\(l,h,a\))에서 6차원(\(l,h,a,f,k,v\))로 늘립니다.
특정 크기가 주어지면 프루닝 방법을 이용해서 정확도를 최대화 하면서, 위에서 제시한 하이퍼파라메터들을 최적화 하는 것이 저자들의 목적입니다. 이렇게 최적화된 모델이 “schuBERT” 입니다.(이유는 모르겠습니다.)
4. schuBERT
schuBERT는 각 디자인 차원에 대응하는 추가적인 학습가능한 메트릭스(변수)를 두어 최적화를 진행합니다. 먼저 각 레이어의 구조는 다음과 같이 일반적인 트렌스포머 블록과 동일합니다. (위가 입력, 아래가 출력입니다.)
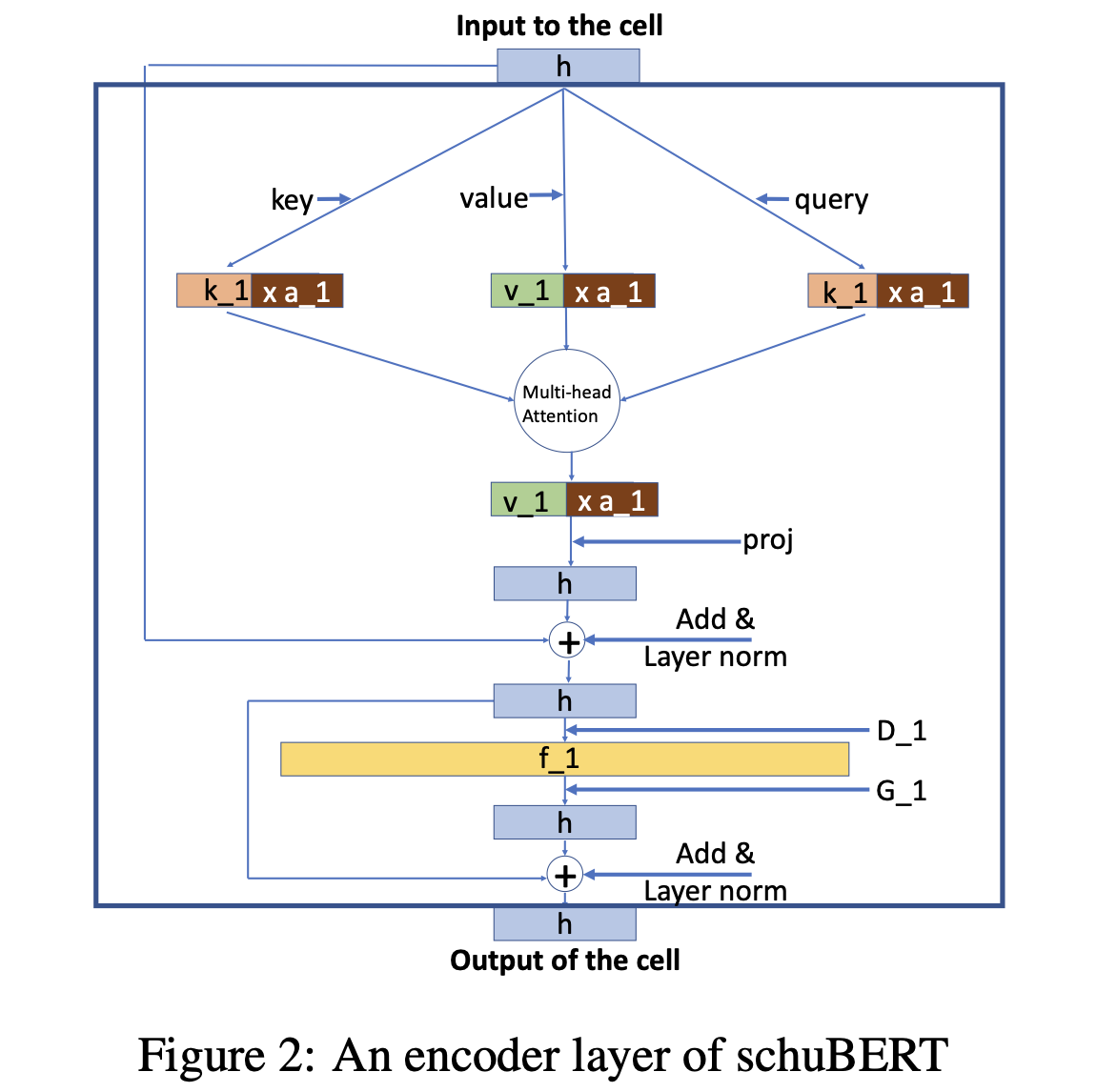
단 “_1”이 붙어 있는 모든 파라메터들은 각 레이어마다 다르게 적용될 수 있는 파라메터를 의미합니다.(즉 그림에서는 1번째 레이어의 구조를 나타내는 것입니다.) 위 그림의 순서를 따라 각 연산들이 어떤 파라메터들을 갖는지 확인해보면 다음과 같습니다.
Multi-head attention은 세개의 파라메터 \(K_1, Q_1, V_1\) 로 구성됩니다. 각 head는 \(K, Q\)를 이용하여 각 토큰 사이의 연관성을 계산하고 이에 따라 \(V\)값을 가중합합니다. (자세한 내용은 Attention is All You Need 논문을 참고해주세요.)
Attetntion 연산을 위한 Key 벡터는 \(a_1\)개의 head에서 \(k_1\) 차원을 갖습니다. 따라서 \(k_1 \times a_1 \times h\) 차원의 파라메터 \(K_1\)을 이용하면 \(h\) 차원의 벡터를 \(a_1\) 개의 \(k_1\) 차원을 갖는 벡터로 projection할 수 있습니다.
Query 벡터는 Key벡터와 내적 연산을 진행하기 때문에 차원이 같아야 하므로 파라메터 \(Q_1\)은 \(K_1\)과 동일하게 \(k_1 \times a_1 \times h\) 차원을 갖습니다.
Value 벡터는 Key-Query 사이에서 계산된 유사도를 바탕으로 가중합될 벡터입니다. 따라서 각 head별로 \(k_1\) 과 분리된 \(v_1\) 차원을 가질 수 있습니다.(head의 수는 같아야 합니다.) \(v_1 \times a_1 \times h\) 차원의 파라메터를 이용하여 projection하여 Value벡터를 얻습니다.
\(K_1, Q_1, V_1\) 3개의 파라메터를 이용한 Multi-head attention은 \(h\)차원의 입력을 \(v_1 \times a_1\) 차원의 출력으로 변환합니다. 이 벡터는 파라메터 \(P_1\)를 이용해서 \(h\) 차원으로 다시 projection 됩니다. 이 결과물에 layer normalization 연산이 적용되고, 초기 입력값과 더해집니다.(residual connection)
위 과정에서 얻은 \(h\) 차원의 출력값은 두 개의 position-wise fully-connected 레이어(\(D_1, G_1\))을 통과합니다. \(D_1\)은 \(f_1 \times h\) 차원, \(G_1\)은 \(h \times f_1\) 차원의 파라메터 입니다. 이 결과물은 layer normalization 연산 후 \(D_1\) 래이어의 입력값과 더해집니다.(residual connection)
여기까지 진행하면 레이어 하나의 연산을 완료하게 됩니다. 이 레이어의 출력값은 마지막 레이어 전까지 다음 레이어의 입력으로 이용됩니다.
위 그림에서 색이 같은 부분은 같은 차원을 가짐을 의미합니다. 즉 \(h\) 는 모든 레이어들에서 같은 차원을, multihead attention에서 각 key와 query는 같은 차원을 가져야 합니다.
추가적으로 ALBERT와 같이 matrix factorization을 이용해 입력 임베딩 크기(\(e\))와 히든 크기(\(h\))가 다를 수 있지만, 본 논문에서는 BERT, XLNET, RoBERTa의 설정과 동일하게 \(e=h\)를 따랐습니다.
5. Optimization Method
5.1. Pruning Parameter
이제 위에서 제시한 각 하이퍼파라메터(디자인 차원)를 어떻게 줄일지 알아보겠습니다. 위에서 잠깐 언급했듯이 본 논문은 프루닝을 이용해서 원래의 BERT-base 구조를 줄여나가고자 합니다. 따라서 각 하이퍼 파라메터들은 BERT-base의 값으로 upper-bound 되고, 1로 lower-bound 됩니다.
각 디자인 차원을 최적화 하기 위해 새로운 프루닝 파라메터 \(\alpha\) 를 제시합니다. pre-trained BERT-base에서 각 디자인 차원에 대응하는 파라메터들(위에서 제시한 \(K, Q, V, P, G\))애 프루닝 파라메터를 곱하고 이를 최적화합니다.
예를 들어 첫번째 레이어의 feed-forward의 경우 시작점은 BERT-base와 동일하게 \(f_1=3072\) 인데, 이를 1로 초기화된 프루닝 파라메터 \(\alpha_{f_1} \in R^{3072}\) 를 이용하여 최적화합니다. 원래의 BERT에서 \(D_1, G_1\) 는 각각 \(f_1\) 과 대응하는데 이를 \(D_1 = D_1 \cdot diag(\alpha_{f_1})\), \(G_1 = G_1 \cdot diag(\alpha_{f_1})\)으로 변경합니다. 각 프루닝 파라메터와 이를 이용한 각 디자인 차원의 파라메터들은 다음과 같습니다.

\(K_i,Q_i\) 는 \(\alpha_{k_i}, \alpha_{a_i}, \alpha_{h}\) 세가지 프루닝 파라메터와 곱해집니다. - key, query 벡터의 크기(\(k_i\)), head 수(\(a_i\)), 히든 크기(\(h\)) 세가지 차원으로 최적화 됩니다.
\(V_i\) 는 \(\alpha_{v_i}, \alpha_{a_i}, \alpha_{h}\) 세가지 프루닝 파라메터와 곱해집니다. - value 벡터의 크기(\(v_i\)), head 수(\(a_i\)), 히든 크기(\(h\)) 세가지 차원으로 최적화 됩니다.
\(D_i, G_i\) 는 \(\alpha_{f_i}, \alpha_{h}\) 두가지 프루닝 파라메터와 곱해집니다. - feed-foward의 크기(\(f_i\)), 히든 크기(\(h\)) 두가지 차원으로 최적화 됩니다.
레이어의 수(\(l\))은 프루닝 파라메터로 프루닝을 진행하지 않는데, \(l\) 에 대해서는 저자들이 여러 실험들을 통해 최적의 값을 정했다고 합니다.
5.2. Pruning Method
프루닝 방법은 프루닝 파라메터를 0으로 치환하는 것입니다. 0으로 치환하면 해당 파라메터에 대응하는 BERT의 파라메터의 행/열이 프루닝 됩니다. (0이 곱해지면 foward/backward 연산에서 영향을 미칠 수 없습니다.) 결과적으로 해당 행/열을 제거하면 파라메터 수가 줄어든 모델을 얻을 수 있습니다. 저자들의 목표는 각 프루닝 파라메터들의 최적화된 값을 찾는 것입니다. 따라서 pretraining loss가 가장 적게 증가하는 파라메터부터 차례대로 프루닝합니다. 구체적인 학습 과정은 다음과 같습니다.
- pre-trained BERT-base(BookCorpus, Wikipedia로 학습된 모델)를 모델의 초기 시작점으로 초기화합니다.
- 프루닝 파라메터를 모두 1로 초기화하고 이를 BERT의 파라메터들에 각각 곱합니다.
- BERT의 파라메터들은 고정하고(아래식의 argmin의 대상은 프루닝 파라메터만 해당함) 다음과 같은 loss로 프루닝 파라메터(\(\alpha\))를 학습합니다. loss는 크게 1) MLM + NSP(BERT의 pretraining loss)와 2) l1 regularization 텀으로 구성됩니다. l1 regularization은 파라메터의 희소성(sparsity)을 유도하기 때문에 각 프루닝 파라메터들이 작아지는 방향으로 학습됩니다. 또한 각 프루닝 파라메터가 0이 되면 BERT의 파라메터 수를 줄이기 때문에 각 프루닝 파라메터에 대응하는 제거될 BERT 파라메터의 수에 비례하는 \(\beta\)를 곱해주어, 각 프루닝 파라메터마다 비슷한 양의 BERT 파라메터를 줄이도록 설정했습니다. \(\beta\) 값은 \(a=1.0, h=0.73, k=0.093, v=0.093, k=0.0078\)을 이용했습니다. \(argmin_{\{\alpha_h,\{\alpha_{a_i}, \alpha_{v_i}, \alpha_{k_i}, \alpha_{f_i}\}\}} \mathcal{L}_{MLM+NSP}(E, \{\tilde{K_i}, \tilde{Q_i}, \tilde{V_i}, \tilde{P_i}, \tilde{D_i}, \tilde{G_i}\})\) \(+ \gamma\{\beta_h \lVert \alpha_h \rVert \} + \gamma\sum\limits_{i=1}^{l}\{ \beta_{a_i} \lVert \alpha_{a_i} \rVert + \beta_{v_i} \lVert \alpha_{v_i} \rVert + \beta_{k_i} \lVert \alpha_{k_i} \rVert+ \beta_{f_i} \lVert \alpha_{f_i} \rVert \}\)
- 위 설정으로 고정된 스탭만큼 학습한 후, 가장 작은 프루닝 파라메터를 0으로 치환하고 해당하는 BERT 파라메터의 행/열을 제거합니다.
- 일반적인 프루닝방법들과 유사하게, 줄여진 파라메터를 갖는 모델을 다음과 같은 BERT의 pre-training loss(MLM+NSP)로 fine-tuning합니다. \(argmin_{\{E, {K_i, Q_i, V_i, P_i, D_i, G_i}\}} \mathcal{L}_{MLM+NSP}(E, \{K_i, Q_i, V_i, P_i, D_i, G_i\})\)
학습 시작 전에 목표하는 모델의 파라메터 수(\(\eta\))를 정해두고, \(T\)번의 스탭을 반복하는데, 각 스탭마다 \(\eta / T\)만큼의 파라메터를 줄여나갑니다. 위의 과정을 요약하면 아래 그림과 같습니다.

6. Experimental Results
6.1. 실험 설정
- regularization step: \(\alpha\)를 학습하는 스탭수 - pre-training에 사용된 스탭의 1/1000
- fine-tuning step: 줄여진 파라메터로 fine-tuning을 진행하는 스탭수 - pre-training에 사용된 스탭의 1/20
- downstream task: SQuAD v1.1, v2.0; GLUE
- model size: 108M(BERT-base)에서 시작해서 99M,88M(BERT \(l=9\)),77M,66M(BERT \(l=6\)),55M,43M(BERT \(l=3\)) 까지 줄임.
- model variation:
- \(\text{schuBERT-x}\): \(x \in \{h, f, a\}\) 각각에 해당하는 하이퍼파라메터만 프루닝한 모델
- \(\text{schuBERT-all}\): \(l\)을 제외한 \(h,f,a,k,v\)를 모두 프루닝한 모델
- \(\text{BERT-all uniform}\): 모든 design dimension을 uniform하게 프루닝한 모델
6.2. 실험 결과
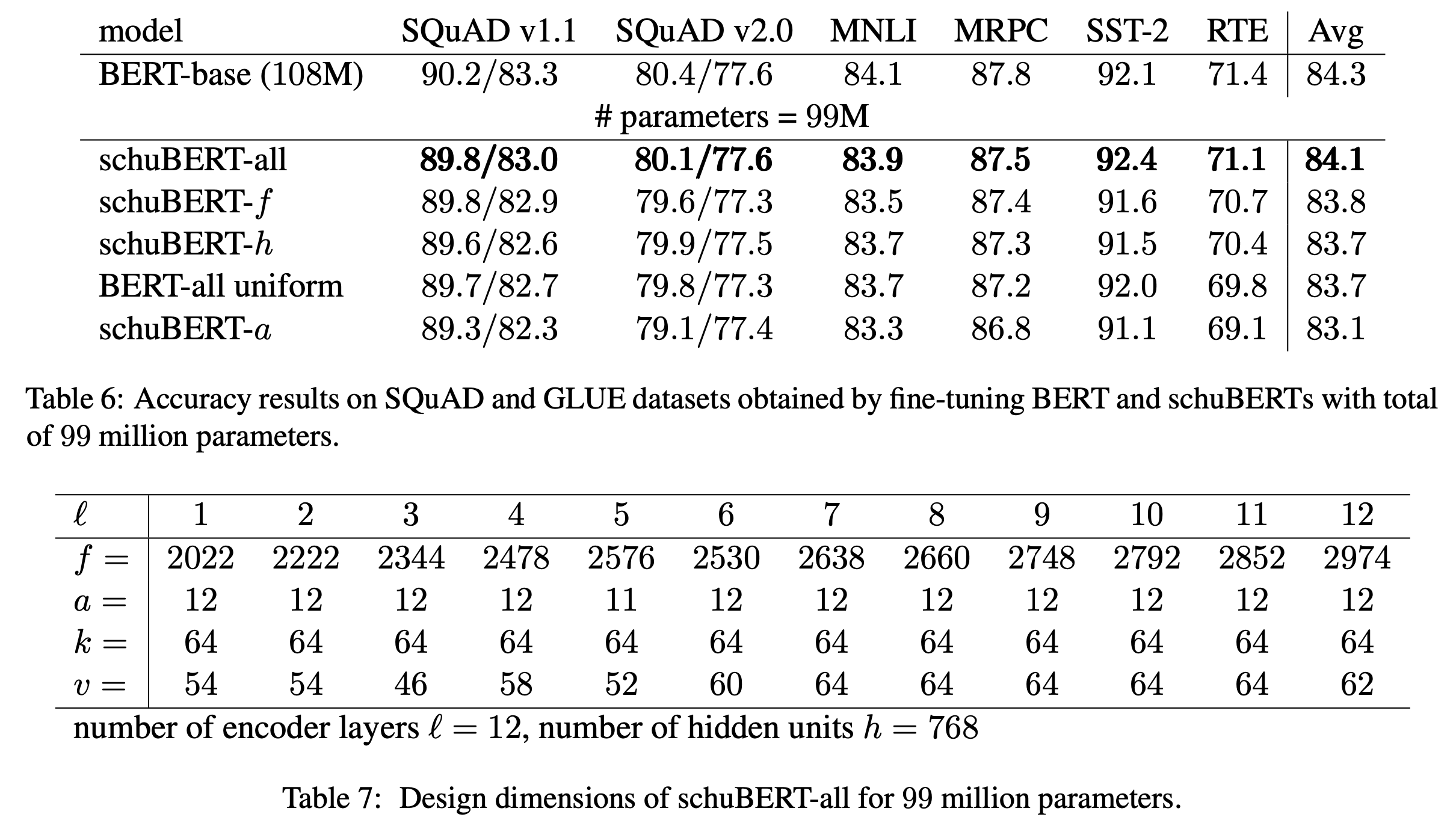
99M 모델의 경우 위의 표(위)와 같이 schuBERT-all이 baseline(BERT-all uniform)보다 0.4높고 BERT-base에 비해 0.2낮은 성능을 보입니다. 위의 표(아래)를 보면, 99M 모델의 각 하이퍼파라메터 차원의 디자인을 보여주는데, \(h,k,a\)는 거의 줄지 않고, 대부분의 파라메터 감소는 feed-forward 레이어(\(f\))로 부터 온다고 볼 수 있습니다. 그리고 \(f\) 의 경우 상위 레이어일수록 증가하는 경향을 보입니다.
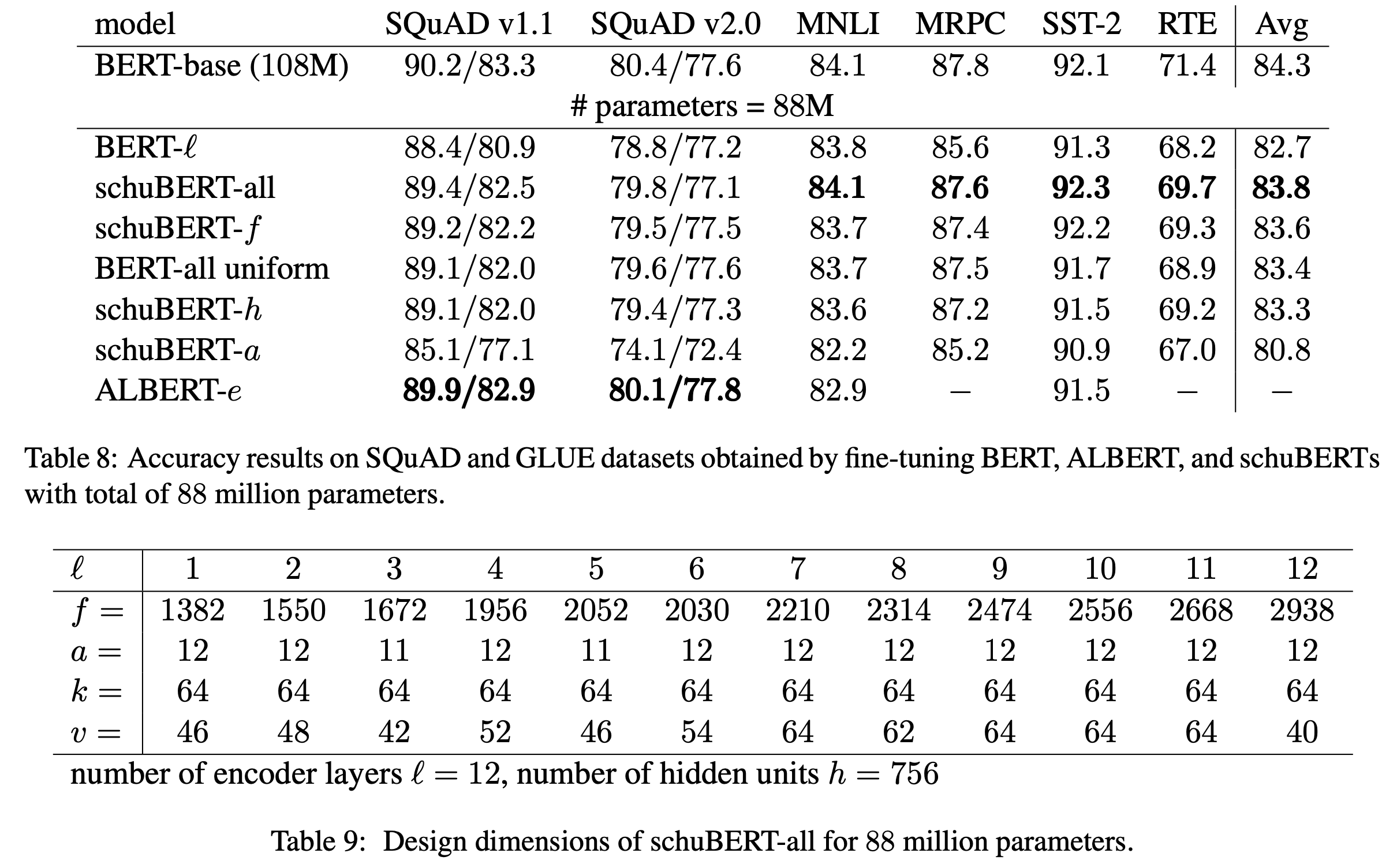
88M 모델의 경우도 마찬가지로 schuBERT-all이 가장 좋은 성능을 보입니다. 특히 \(l=9\)인 BERT모델에 비해 1.1 정도 높은 성능을 보여줍니다. 하이퍼파라메터의 경향성도 99M 과 비슷하게 나타납니다.
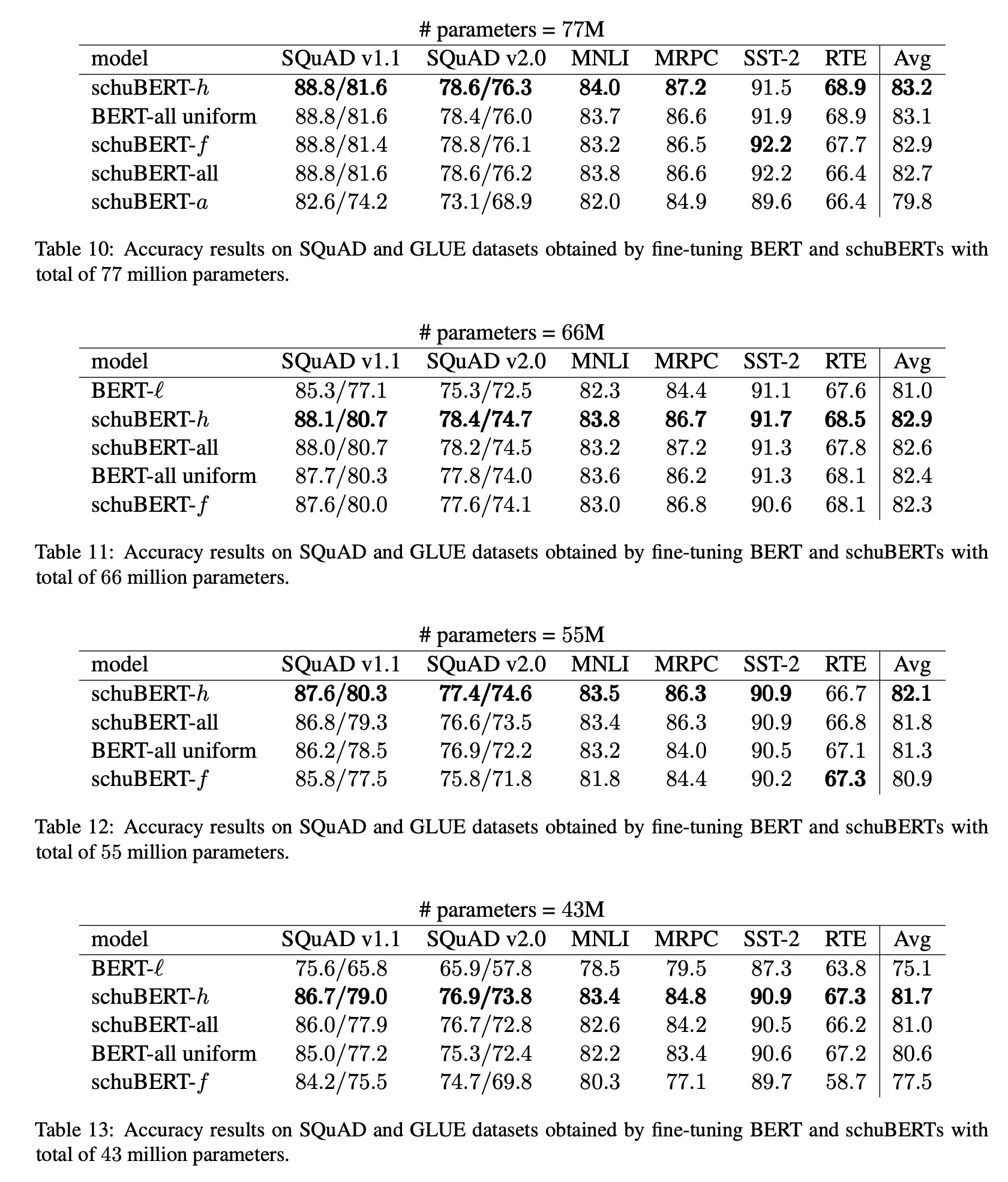
77M, 66M, 55M, 43M 모델의 결과는 위의 표와 같습니다. 이상적으로, schuBERT-all이 가장 좋은 결과를 보일 것으로 기대할 수 있지만, 사이즈가 작아질수록 schuBERT-h가 좋은 성능을 보여줍니다. 저자들은 이 이유를 schuBERT-all은 많은 디자인 차원들을 프루닝하는 것은 복잡도가 높기 때문으로 예측합니다. schuBERT 66M 모델의 경우, \(l=6\)인 BERT모델에 비해 1.6 높은 성능을 43M 모델의 경우, \(l=3\)인 BERT모델에 비해 6.6 높은 성능을 보여줍니다. 이를 통해 가벼운 BERT를 만들기 위해서는 레이어 수를 줄이는 방향 보다 히든 유닛들의 수를 줄이는 방향으로 진행되어야한다는 것을 알 수 있습니다.
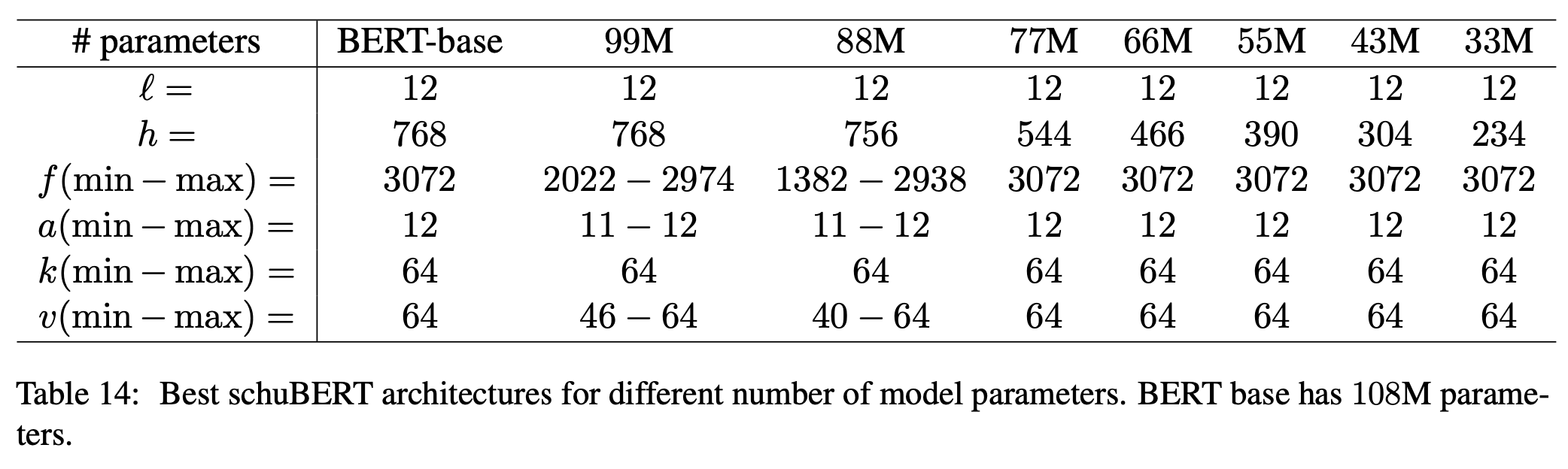
위 표는 각 크기의 schuBERT에서 가장 좋은 구조를 보여줍니다.
7. Conclusion
위의 결과를 통해 schuBERT 구조 디자인 차원에 대해 다음의 인사이트를 얻을 수 있습니다.
Slanted Feed-forward Layer: 각 토큰 별로 적용되는 feed-forward 레이어의 경우, 상위레이어로 갈수록 비교적 중요한 역할을 합니다.
Tall and Narrow BERT: 더 가벼운 모델을 얻고 싶은 경우, “tall and narrow” 즉 깊고 얇은 구조를 선택하면 얕고 넓은 구조에 비해 더 좋은 결과를 기대할 수 있습니다. 위의 결과에서 동일한 파라메터 수의 schuBERT l=12 가 BERT l=3,6,9를 큰 격차로 능가하는 모습을 볼 수 있습니다.
Expansive Multi-head Attention: BERT는 key, query, value 벡터의 차원을 \(h/a\)로, feed-forward filter의 크기를 \(4f\)로 고정하고 있습니다. 하지만 Multihead Attention 연산 자체는 다른 \(k, v, f\)를 이용하는데 제약이 없습니다. 실험 결과 모델 크기가 작아질수록 히든 크기가 줄어도 key, query, value의 차원은 줄어드지 않음을 볼 수 있습니다. 즉 위 표에서 43M 크기 모델의 경우 \(h=304\) 이므로 \(h/a=25.3\) 정도 이지만 실제로 \(k, v = 64\)임을 볼 수 있습니다. 또한 \(f=4h=936\) 이지만 실험 결과 \(f=3072\)입니다. (사실 이 점은 \(h\) 만 프루닝 했기 때문이기도 합니다.) 결과적으로 모델의 크기가 줄어들수록 Multihead Attention의 파라메터를 많이 살리면(expansive) 성능을 잘 보존할 수 있습니다.
